Come spiego i miei interessi a mia mamma?
Inizio col dire che i miei interessi si collocano nell'intersezione di tre rami della matematica: topologia, geometria e algebra.
Di cosa si occupano queste branche?
- Presi due punti distinti, riusciamo a dire quanto sono lontani?
- Esiste una nozione di "andare dritto"?
- Esiste una nozione di angolo che generalizza quella usuale? Se si, come possiamo misurare questi angoli?
- Come sono fatti i triangoli in contesti diversi?
Topologia
La topologia è un ramo della matematica che studia la "forma" di alcuni oggetti. Non c'è un significato univoco di "forma", si potrebbe dire che il significato che gli diamo è proprio ciò che distingue topologia e geometria.
La topologia è una parente "grossolana" della geometria, e gli oggetti che si studiano non sono dotati di quella che nella vita di tutti i giorni chiameremmo "forma", ma più propriamente con una nozione astratta di "vicinanza".
Questa ci permette di definire cosa sia una funzione continua, cioè una funzione che non "strappa" gli oggetti che studiamo.
Immaginatevi di star giocando con un pezzo di plastilina: potete tirarlo, allungarlo, schiacciarlo (non troppo), ma non potete tagliarlo, bucarlo o incollare due pezzi.
Se per esempio partite da una pallina, la potete allungare e farci un cilindro, ne potete fare un cubo, una piramide, un icosaedro; non potete, però, incollare due estremità del cilindro per formare una ciambella. Potete prendere la ciambella (o toro, come si dice), e farne una tazza:

A questo punto, in maniera naturale viene in mente una domanda: Riusciamo a dire che una sfera non è un toro?
Qui ci viene in aiuto la profonda interazione con l'algebra: se intuitivamente è chiaro che non lo siano, visto che un toro non è altro che una sfera con un buco scavato al centro (cosa che abbiamo detto non essere ammissibile), dimostrarlo rigorosamente è tutta un'altra storia.
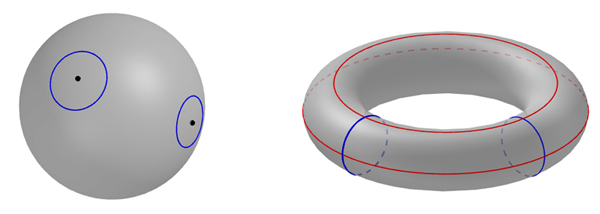
Facciamo un esperimento mentale: siete sulla superficie di un toro o di una sfera, insieme al vostro cane, ma non sapete dove, e vi viene chiesto di determinarlo. Come potete fare?
Non c'è un'unica risposta corretta, ma un metodo possibile è il seguente: fate camminare il vostro cane liberamente (tenendolo legato con un guinzaglio infinito). Appena il cane ritorna da voi, tirate il guinzaglio: se si incastra da qualche parte, sapete con certezza di trovarvi sulla superficie del toro.
Nel linguaggio della topologia, diciamo che un toro ammette lacci omotopicamente non banali, mentre la sfera no. Equivalentemente, la sfera ha gruppo fondamentale banale, il toro no.
In una formula, \[\pi_1(S^2)=0, \quad \pi_1(S^1\times S^1)\neq 0.\]
Geometria
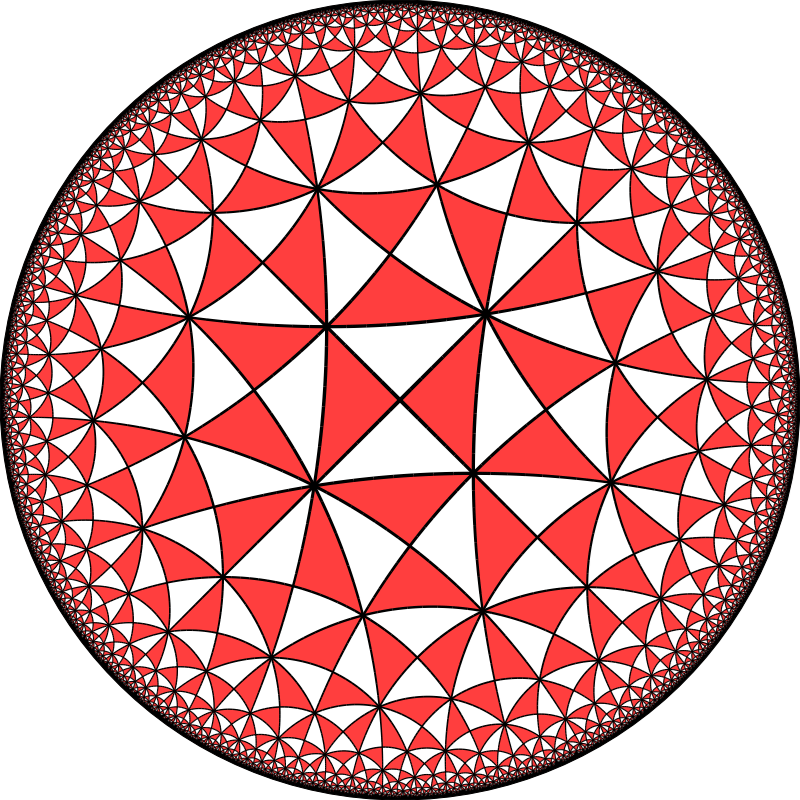
La geometria studia strutture molto più ricche, come metriche e connessioni. Mentre la topologia studia un concetto debole di "vicinanza", le strutture più precise della geometria danno un senso alle seguenti domande (tra molte altre), cosa altrimenti impossibile:
L'interazione tra geometria e topologia sta al cuore delle due discipline, e alcune delle domande più complesse di una possono trovare risposta usando tecniche e oggetti dell'altra: l'esempio più famoso è probabilmente la cosiddetta congettura di Poincaré, un problema puramente topologico che fu risolto usando strumenti e tecniche geometriche.
Algebra
L'algebra è un ramo della matematica che, nella sua forma più pura, studia l'origine di pattern e relazioni provenienti da strutture a priori diverse.Per esempio, prendete un cubo di Rubik, e numerate i quadretti che ne compongono le facce. Le mosse possibli si possono comporre una con l'altra, sono tutte reversibili, e c'è una mossa che lascia fisso ogni quadretto (basta non fare nulla). Diciamo che queste mosse formano un gruppo.
La grande forza dell'algebra è togliere ogni tipo di significato materiale agli oggetti (in questo caso, le mosse sul cubo diventano elementi di un oggetto astratto), e studiarli da un punto di vista puramente formale. Questo ci permette di capire quali regole vengono rispettate da oggetti materialmente diversi, ma che possiedono la stessa struttura basilare.
Perché ti dovresti interessare alla matematica?
Inizio col dire che non devi interessarti alla matematica.
Voglio anche dire però che il pattern più ricorrente nella storia della disciplina è quello di un'idea che in principio viene ritenuta inutile, salvo trovare applicazione tempo dopo, magari in una diversa disciplina, o in un campo diverso. Per citare un paio di esempi recenti:
- Gli antichi greci studiavano la distribuzione dei numeri primi già 2500 anni fa. Il metodo crittografico RSA, inventato nel 1977, fa affidamento sul fatto che i numeri primi siano sufficientemente sparsi da rendere impossibile la fattorizzazione di un numero grande in tempo utile. Ad oggi, è uno dei metodi più usati per compiti di cifratura e decifratura in massa.
- Nel 1854 George Boole, un autodidatta inglese, pubblicò un libro contenente la sua teoria algebrica del calcolo logico. Largamente ignorato dai contemporanei, il suo lavoro fu riscoperto con l'avvento dei primi computer elettronici, circa 100 anni dopo, ed è oggi considerato il principio della moderna teoria della computazione.